Spatio-temporal/time-series data analysis

In our society, large quantities of data are collected and recorded. However, there are many undeveloped areas in the handling of mass data, and such data is not fully utilized. In my research, I find new information among such diverse sets of data and develop methods of prediction. I also carry out joint research with researchers in a variety of fields aimed at the application of data to real-world problems.

In particular, one of my research themes, “Bayesian statistics” (*1), is effective in analyzing spatio-temporal data captured by a sensor or a camera, such as weather information, and time-series data that changes from moment to moment, such as stock prices and exchange rates. Together with researchers from various fields, we are looking for ways to interpret what has occurred, what information is hidden, and what may happen in the future.

In a recent joint endeavor with a researcher in biology, we estimated the hardness of cell membranes as time advanced based on cell microscope data. We also conducted research, based on tide gauge data acquired at the time of the 1993 Hokkaido Earthquake, to evaluate how the bottom topography influences the reproduction of tsunami simulations. A tsunami travels faster offshore and then slows down in coastal areas. In other words, a wave travels faster in areas where the water is deep and it slows down in shallow water. This means if precise data on the bottom topography is available, it is possible to predict the arrival time and the conditions regarding a tsunami with a high level of accuracy. This information is useful from the oceanographic point of view. For example, it enables the simulation of ocean currents and the prediction of the route of a shipwreck based on simulated currents.

In a related field, my laboratory is also engaged in research analyzing how a tsunami inundates the land. The goal of this research is to detect and inform people as accurately and quickly possible of areas where seawater intrusion can be expected when a tsunami occurs. This research is based on published tsunami trace data at the time of the Great East Japan Earthquake. Considering the current quantity of data, this data is not big data. However, a large number of videos of the tsunami were recorded at the time of the Great East Japan Earthquake and these videos contain more useful information than just the traces of the tsunami. Our next challenge is the analysis of this video data. We need to handle it with great care since this data may be too large for the phenomenon to be analyzed.

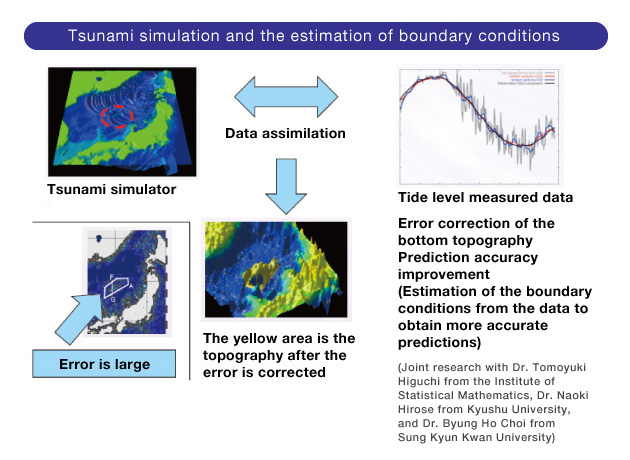
Retrieving valuable information from large quantities of data

We are studying economic data in which abrupt fluctuations in exchange transaction rates are automatically picked up to indicate whether it is either a stable or an unstable index. Behind this study is the fact that stock and currency exchanges have been conducted at very short time intervals in recent years, and thus it has become very difficult to follow the movement of stock prices or exchange rates. In today’s markets there exists a tremendous amount of transaction data containing a great number of small price fluctuations. Our goal is to develop a tool that can stochastically indicate which price fluctuations, among all those small fluctuations, may or may not have a major impact on the market so the national government or the institution can draft an effective plan before the financial market panics. In fact, the yen drastically depreciated in foreign exchange markets immediately after the Great East Japan Earthquake, and we were able to quickly detect the unstable market conditions based on the data and the hypothesis. Unstable market conditions subsequently continued, but then suddenly the yen got stronger. This study requires online processing of large quantities of real time data, and in this sense, this is big data analysis. Conventional analytical tools were developed on the premise that such large quantities of data could not be obtained. But new technology will be needed as mass data acquisition has become possible.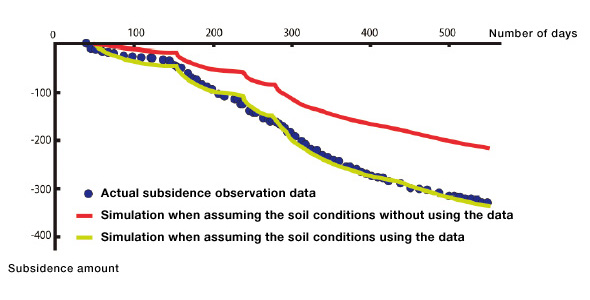

Joint research on geotechnical problems. Although the amount in the soil is difficult to measure, it has been verified that using data assimilation methods can improve prediction accuracy.

A mathematical theory that supports big data

Along with “Bayesian statistics,” another key research theme of mine is “data assimilation” (*2). Data assimilation is technology derived from meteorology and it can enhance the accuracy of simulation results to the greatest possible extent by balancing data from the real world and simulated data on a computer, using mathematical methods.

In joint research on geotechnical problems, we predicted possible ground subsidence, using this data assimilation method. If we continue advancing the development of this technology, we will be able to provide beneficial information to address various problems, such as the maintenance of aging infrastructure that was developed during periods of high economic growth. For instance, we will be capable of stochastically predicting the service life of bridges and expressways, and setting rough priorities for maintenance work based on probability. Although we cannot make precise predictions about the service life of aging infrastructure, we can provide information on the probability of different scenarios while enhancing the accuracy of predictions using data analysis and mathematical theory. Of course, people are the ones who make such decisions. It is up to the people concerned whether or not they proceed with maintenance from the viewpoint of cost. However, they can take our prediction into account as they make these decisions. I think that in this way our research can find common ground in the society.

I believe big data can serve many purposes in business. The more information you have, the greater the competitive advantage you gain – there is no doubt about that. Data will continue to increase in volume, and the cost of collecting data will continue to drop. However, how data will be used is not yet widely known. The key to the development of this field lies in an increase in the number of people who understand correctly how big data is supported by mathematical theory and the areas of analysis in which big data is effective. I will contribute my humble efforts to ensure that “big data” does not end up as just a buzz word as I offer lectures on big data in adult education classes at the Liberty Academy, Meiji University.

Show shortcuts through theoretical studies

In order to effectively use big data, the revision of data assimilation methods from the theoretical point of view in statistics is another challenge. This revision will allow us to provide feedback on the current data assimilation techniques and make them easier to use. Researchers in mathematical sciences, including statistics, should consciously organize, from the viewpoint of mathematical sciences, the analytical methods and knowledge acquired through the results of the assiduous efforts of people in the field, and share with them “easier ways” and “new solutions that they have overlooked.” For instance, real weather prediction is a world of super big data where sequential observation data is collected from a meteorological satellite and weather stations. I devised an analytical method that can be used in such an environment, while at the same time, I analyze large accumulations of data in the world, retrieve information hidden in the data, predict the future, and discover what is beneficial – this is my research.

Profile

Associate Professor, Department of Mathematical Sciences Based on Modeling and Analysis, School of Interdisciplinary Mathematical Sciences
Research interest: Statistical Science, especially Bayesian Statistics and its Application to Spatio-Temporal Analysis, Data Assimilation

Project Researcher, CREST, Japan Science and Technology Agency
Project Researcher, the Institute of Statistical Mathematics, Research Organization on Information and Systems
Lecturer, Organization for the Strategic Coordination of Research and Intellectual Property, Meiji University, 2009
Lecturer, Graduate School of Advanced Mathematical Sciences, Meiji University, 2011
Associate Professor, School of Interdisciplinary Mathematics, Meiji University, 2013
Ph.D., Department of Statistical Sciences, Graduate University for Advanced Studies (Sokendai)

(*1) Bayesian statistics
Bayesian statistics is a method of calculating the probability of hidden information and uncertain phenomena behind data using “Bayes’ theorem.” Classical statistics requires high-quality random samples, and it is also difficult to incorporate known information into statistical framework. However, Bayesian statistics can solve these problems, and can provide validity to the inference led by a small number of samples or a large number of samples that are heterogeneous in quality. Familiar examples of applications using Bayesian statistics include spam e-mail filters, speech recognition for mobile phones, and the predictive conversion of Japanese input characters into words.

(*2) Data assimilation
A method in which actual observations and measured data are incorporated into computer simulations. Numerical simulations generate a variety of scenarios depending on how the initial conditions, boundary conditions, or parameters are determined. Therefore, this method aims to increase the accuracy and performance of simulations by incorporating actual data. In recent years, data assimilation has been closely watched in the field of simulation science. Data assimilation research teams and centers have been formed at various research institutions and universities, and data assimilation has been used in their research projects.