プレスリリース

・タンパク質の大きさを表す慣性半径R_gが1/fゆらぎを示します。
・溶媒中でのタンパク質の拡散性が時間的に変動し、各時刻における拡散性の大きさがその時のタンパク質の大きさ（慣性半径R_gと水和層の大きさR₀の和）の逆数に比例するというストークス・アインシュタインの式を拡張した形で記述できることを明らかにしました。
タンパク質はアミノ酸が紐状に繋がったものです。タンパク質は、溶媒中では折りたたまれたり解けたりを繰り返しながら存在しています。いわば、紐が伸びたり縮まったりを繰り返している状態です。アミノ酸配列の違いにより、折りたたまれる構造は多岐にわたり、また、構造が変化する時間スケールも様々です。時間経過とともに構造が複雑に変化するタンパク質は、溶媒中でどのように拡散するのか？どの様な物理法則が存在するのか？という問いが興味深い問題となっています。近年の計算機能力の向上により、タンパク質構造の時間変化を分子レベルで直接追うことが可能になり、構造変化と拡散性の関係をシミュレーションにより明らかにすることが現実的になってきています。
溶媒中でのコロイド粒子などの微粒子は、溶媒から受けるランダムな力によって、ブラウン運動と呼ばれる不規則な運動を行います。このブラウン運動がどの程度の速さで拡散するのかを定量化した拡散係数は、粒子の形状や溶媒の性質で決まります。特に、この拡散係数Dが粒子半径Rの逆数に比例するストークス・アインシュタインの関係式が知られています。この式では、粒子の大きさは常に一定で、拡散係数も一意に決まります。しかし、タンパク質はきれいな球形ではない、かつ、立体構造が時間とともに複雑に変化してしまうため、この式をそのまま適応することができませんでした。
本研究では、頻繁に構造が変化するタンパク質とあまり変化しないタンパク質のいくつかについて分子動力学シミュレーション（※2）を行い、タンパク質構造と拡散性の時間的なゆらぎについて解析しました。これまで、構造が複雑で大きなタンパク質については、立体構造のゆらぎに長期的な相関が現れることがわかっていました。本研究では、比較的小さく、構造がシンプルなタンパク質についても、タンパク質の大きさを表す慣性半径（R_g）が長期相関（1/fゆらぎ）を示すことを明らかにしました。
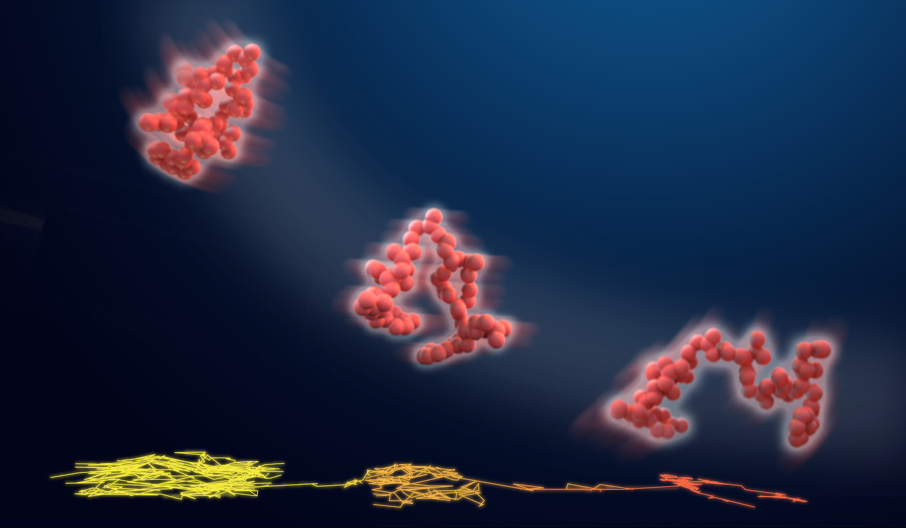
次に、拡散係数の時間変化を推定する手法を用い、時間経過とともに変化する拡散係数D_Iの切り替わりを推定し、D_Iが顕著なゆらぎを示すことを観測しました。この拡散係数D_Iの大きさは、タンパク質の大きさ（慣性半径R_gとタンパク質表面に強く結合している水分子の厚みR₀（~0.3 nm）の和）の逆数と相関があることがわかりました。つまり、タンパク質の構造が伸びて大きくなるほど拡散性が小さく、構造がコンパクトに縮まるほど拡散性が大きくなることを意味しています（図1）。この関係は本研究で対象としたすべてのタンパク質、様々な温度・圧力条件でも成り立ちます。また、タンパク質の構造が大きく変化するのに要する時間と拡散係数が大きく変化するのに要する時間が同じオーダーであることがわかりました。 図1:溶媒中におけるタンパク質の大きさと拡散係数の関係性（D_I ∝ 1/[R_g + R₀]）を表した概念図。シミュレーションに用いたタンパク質は、アミノ酸残基が10残基のChignolin、35残基のVillinやPin1 WWドメイン。
細胞内における生体分子の拡散現象は、生体反応などの制御に関わり、細胞機能の維持において重要です。実際の細胞内では、様々な生体分子がひしめき合う複雑な環境になっており、そのような場での拡散現象においてもR_gとD_Iの関係が成立するのか、興味は尽きません。
Eiji Yamamoto, Takuma Akimoto, Ayori Mitsutake, and Ralf Metzler, Universal relation between instantaneous diffusivity and radius of gyration of proteins in aqueous solution, Physical Review Letters (2021).
doi: https://doi.org/10.1103/PhysRevLett.126.128101
Physics “Shape-Shifting Proteins Follow Diffusion Rules”
https://physics.aps.org/articles/v14/s32
※1　溶媒中での球体の拡散現象において、拡散係数Dが球体の半径Rに反比例するという関係式、D = k_BT/6_πηR。ここで、k_Bはボルツマン定数、Tは温度、ηは粘度。
※2　分子動力学シミュレーション：粒子の動きをコンピュータ上で模擬する手法。古典力学におけるニュートンの運動方程式を数値的に解くことで、時々刻々の粒子の動きを知ることができる。

※ご取材の際には、事前に下記までご一報くださいますようお願い申し上げます。
※本リリースは文部科学記者会、科学記者会、各社科学部等に送信させていただいております。